Оригинал статьи под авторством Robin Thomas.
Эта страница дает краткий отчет, о новом доказательстве
Проблемы четырех красок и алгоритме четырех цветов найденых Нилом Робертсоном, Даниэлем П. Сандерсом, Полом Сеймуром и Робином Томас.
Содержание
1..История.
2. Зачем нужно новое доказательство?
3. Краткое описание доказательства.
4. Основные принципы доказательства.
5. Конфигурации.
6. Выполнение правил.
7. Указатели.
8. Квадратичный алгоритм.
9. Обсуждение.
10. Список литературы.
История.
Проблема четырех красок достигает 1852 года, когда Фрэнсис Гатри, пытаясь нарисовать карту Английских графств, заметил, что достаточно четырех цветов. Он спросил своего брата Фридриха, правда ли, что любая карта может быть окрашена с использованием четырех цветов таким образом, чтобы прилегающие регионы (т.е. те, которые имеют общие пограничные участки, а не только точку) имели разные цвета. Затем Фредерик Гутри передал гипотезу Деморгану. Первое печатное упоминание относится Кейли в 1878 году.
Через год появилось первое «доказательство» Кемпе. Его ошибочность была отмечена Хейводом 11 лет назад. Другое неудачное доказательство согласно Тейту в 1880 году — пробел в выводе, указанном Петерсеном в 1891 году. Однако оба неудачных доказательства имели определенную ценность. Кэмпе открыл то, что стало известно как цепочки Кэмпе, а Тейт нашел эквивалентную формулировку четырехцветной теоремы в 3-цветной рёберной окраске.
Следующий крупный вклад был сделан Биркгофом, работа которого позволила Франклину в 1922 году доказать, что гипотеза четырех цветов верна для карт с не более чем 25 регионами. Её также использовали другие математики, чтобы создавать различные форм прогресса для проблемы четырех красок. Мы должны особым образом упомянуть Хеша, который разработал два основных компонента, необходимых для окончательного доказательства — сокращение и освобождение. Хотя концепция сокращения изучалась и другими исследователями, идея освобождения, имеющая решающее значение для неизбежной части доказательства, связана с Хешем. Именно он предположил, что подходящая разработка этого метода решила бы проблему четырёх красок.
Это было подтверждено Аппелем и Хакеном в 1976 году, когда они опубликовали своё доказательство Проблемы четырёх красок.
Зачем нужно новое доказательство?
Существует две причины, почему доказательство Аппеля-Хакена до конца не подходит. Часть доказательства Аппеля-Хакена провели с помощью компьютера и её нельзя проверить вручную — даже та часть, которую предположительно можно проверить вручную, чересчур сложная и утомительная, и насколько нам известно, никто так полностью её и не подтвердил.
На самом деле, мы пытались подтвердить доказательство Аппеля-Хакена, но вскоре сдались. Проверка компьютерной части требует не только много программирования, но и учёт описания 1476 параграфов. А это даже не была спорная часть доказательства. Мы подумали, что будет гораздо выгодней, разработать наше собственное доказательство. Мы так и сделали, и получили доказательство, описанное ниже.
Основные принципы.
Основная идея доказательства такая же, как у Аппеля-Хакена. Мы обнаружили набор из 633 «конфигураций» и доказали, что каждая из них «сокращаема». Эта техническая концепция подразумевает, что ни одна конфигурация с таким свойством не может появиться в минимальном контрдоказательстве Проблемы четырёх красок. Её так же можно использовать, как алгоритм,
поскольку конфигурация сокращения появляется в пленарной графе G и тогда, в течении постоянного времени, можно построить пленарную графу G поменьше, так что любая четырёхцветная G может быть преобразована в четырёхцветную G линейного времени.
С 1913 года известно, что каждое минимальное контрдоказательство, применяемое к Проблеме четырёх красок, является внутренне 6-связанной триангуляцией. Во второй части доказательства, мы доказываем, что хотя бы одна из наших 633 конфигураций появляется в каждой внутренней 6-связанной триангуляции (не обязательно минимальный контрпример к 4CT). Это называется доказательством неизбежности, где используется «метод освобождения», впервые предложенный Хешем. Тут, наш метод отличается от предложенного Аппелем и Хакеном.
Основные принципы доказательства.
Мы подтверждаем гипотезу Хеша о том, что используя доказательство неизбежности, можно найти конфигурацию сокращения во второй окрестности «перегруженной» вершины. Таким образом, мы избегаем «иммерсионных» проблем, которые были основным источником осложнений для Апреля и Хакена. Наша конфигурация неизбежности размером 633, противоположна 1476 звеньевой конфигурации Аппеля и Хакена. А наш метод освобождения использует только 32 правила освобождения, вместо 300+ Аппеля и Хакена. И наконец, мы получаем квадратичный алгоритм четырёхцветного планарный графа (который будет описан позже), улучшение уравнения четвёртой степени Аппеля и Хакена.
Конфигурации.
Почти триангуляция является без нулевым, без петельным планарным графом, так что всякая бесконечная область является треугольником. Конфигурация K состоит из почти триангуляции G, а координата g из V(G) переходит в целые числа с следующими свойствами:
Для каждой вершины v, G\v в большинстве имеет два компонента, а если их два, то степенью v является g(v)-2,2.
Для каждой вершины v, g(v) равно степень v, при условии, что v не случайно находится в бесконечной области. В противном случае g(v) больше, чем степень v, и в обоих случаях g(v)> 4,
Кольцевой размер K, как минимум 2, где кольцевой размер K определяется как сумма g(v)-deg(v)-1, суммируемая по всем вершинам v, свойственным бесконечной области, такой, с которой связан G\v.
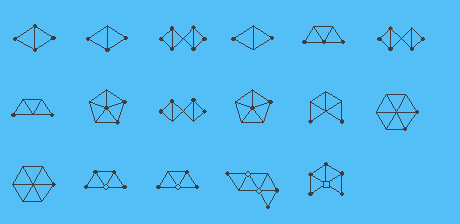
При рисовании схем конфигураций, мы используем гипотезу Хеша. Формы вершин показывают значение g(v) в следующем виде: массивный, чёрный круг означает g(v)=5, точка (или то, что показано на картинке без символа вовсе) означает g(v)=6, кольцевое сечение означает g(v)=7, квадратное сечение означает g(v)=8, треугольник означает g(v)=9, а пятиугольник g(v)=10. (Нам не нужна вершина v, где g(v)> 11 и только одна вершина g(v)=11, для которой мы не используем никаких особенных символов). На схеме ниже, 17 из наших 633 сокращаемых конфигураций показаны с использованием indicated convention. Полный набор можно увидеть, нажав тут . (Мы ссылаемся на пункт (3.2) нашего документа для значения «жирные рёбра» и «полурёбра».
Работоспособной конфигурацией называется, любая конфигурация, сходная по структуре одной из 633 конфигураций , показанных в 7. Допустим T — это триангуляция. Конфигурация T является K=(G,g), если G это индуцированный подграф T, каждая конечная область G является областью T, а g(v) равняется степени v в T для каждой вершины v из T. Мы доказали два следующих
высказывания.
Теорема 1. Если T является минимальным контрдоказательством Проблемы четырёх красок, тогда у T не существует работоспособной конфигурации.
Теорема 2. Для каждой внутренне 6-связанной триангуляции T, существует работоспособная конфигурация T.
Из двух, вышеуказанных теорем следует, что ни одно минимальное контрдоказательство не существует, а 4CT является настоящим. Для первого доказательства нужен компьютер. Второе можно проверить вручную за несколько месяцев, а если использовать компьютер, то за 20 минут.
Выполнение правил.
Допустим, T является внутренне 6-связанной триангуляцией. Первоначально, каждая вершина v определяет заряда 10(6-deg(v)). Из формулы Эйлера следует, что сумма зарядов всех вершин равна 120. По сути, она положительна. Сейчас мы перераспределяем заряды согласно следующим правилам таким образом. В каждом случае, когда T имеет подграф, изоморфный одному из графов на рисунке снизу и удовлетворяющий степень детализации (для вершины v, как правило, со знаком минус, это означает, что степень соответствующей вершины T не больше, заданого формой v, и аналогично для вершин со знаком плюс; для вершин, не имеющих знака рядом с ними, требуется равенство), заряд одного (или двух, при применении первого правила) должен быть отправлен по краю, отмеченному стрелкой.
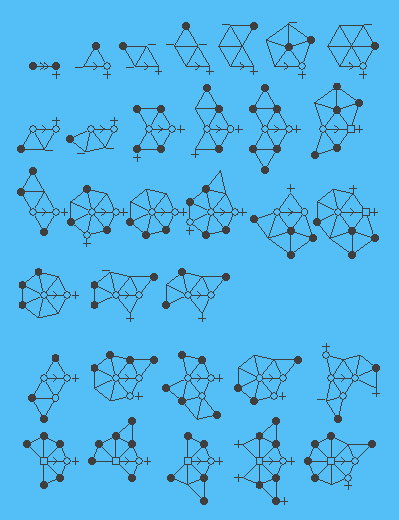
Эта процедура определяет новую группу зарядов с одинаковой суммой. Так как полная сумма положительная, то вершина v в T, чей новый заряд положительный. Мы демонстрируем, что работоспособная конфигурация появляется во второй окрестности v. Если степень v не более 6 или не менее 12, тогда это можно легко увидеть под прямым аргументом. Однако для остальных случаев доказательства гораздо сложнее. Поэтому, мы написали доказательство формальным языком, чтобы его можно было проверить через компьютер.
Каждый отдельный шаг этих доказательств проверяется людьми, но сами доказательства нельзя проверить вручную из-за их длины.
Указатели.
Теоретическая часть нашего доказательства описана в 7.
Десяти страничный опрос доступен онлайн. Компьютерные данные и программы раньше находились на анонимном ftp сервере, но от него постепенно отказались. Сейчас эти же файлы доступны на
http://www.math.gatech.edu/~thomas/OLDFTP/four/ и их можно удобно просмотреть. Независимый набор программ был написан Гаспером Фиявзом под руководством Бояна Мохара.
Квадратичный алгоритм.
Исходный алгоритм будет плоской триангуляцией G с вершинами n. (Без потери общности, так как любой планарный граф может быть триангулирован в линейном времени.) Результатом будет окрашивание вершин G четырьмя цветами.
Если у G не более четырёх цветных вершин, то у каждой вершины будет разный цвет. В другом случае, если степень G минимум 5. Мы вычислили заряд каждой вершины, как показано выше, и определили вершину v с положительным зарядом. Из нашей Теоремы 2 следует, что как работоспособная конфигурация, находящаяся во второй окрестности v (в случае, когда её можно найти в линейном времени), так и k-кольцо, нарушающее определение внутреннего 6-соединений, можно найти в линейном времени. В последнем случае, мы прибегаем к кольцевому k-кольца ниже, а в первом мы применяем рекурсию к конкретному малому графу. Окрашивание G в четыре цвета может быть сконструировано из четырёхцветного окрашивания меньших графов в линейном времени.
Можно применить процедуру, разработанную Биркгофом, учитывая, что k-кольцо R, нарушающее определение внутреннего 6-соединения. Мы применяем рекурсию к двум тщательно подобранным подграфам G. Тогда четырёхцветность G может быть построена по четырёхцветности двух других графов в линейном времени.
Дискуссия.
Должны упомянуть, что обе наши программы используют только арифметическое устройство для работы с целыми числами, поэтому нам не нужно беспокоиться про ошибки округления и аналогичные опасности арифметической операции с плавающей запятой. Тем не менее, можно утверждать, что наше «доказательство» не является доказательством в традиционном смысле, поскольку оно содержит шаги, которые никогда не смогут быть проверены людьми. В частности, мы не доказали правильность компилятора, на котором мы составили наши программы, и
не доказали безошибочность оборудования, на котором мы их запускали. Их стоит принять на веру, ведь, предположительно, они являются источником ошибок.
Однако с практической точки зрения вероятность ошибки компьютера, которая выглядит одинаково на всех прогонах наших программ и компиляторах, во всех операционных системах, на которых работают наши программы, бесконечно мала по сравнению со случайностью человеческой ошибки при таком же количестве проверки. Помимо этой гипотетической возможности, что компьютера постоянно будет давать неверный ответ, остальное наше доказательство можно проверить так же, как и традиционные математические доказательства. Однако мы признаем, что проверка компьютерной программы гораздо сложнее, чем проверка математического доказательства той же длины.

Добавить комментарий