У квітневому номері 1975 року, Мартін Гарднер — американський науковий співробітник у колонці «Математичні ігри» опублікував список 6 основних математичних відкриттів 1974 р, які «з тієї чи іншої причини були недостатньо висвітлені як науковому співтовариству, так і громадськості в цілому». Одним з них був планарний граф з 110 вузлів, приписаний Вільяму МакГрегору з Уонпінгерс Фолз, штат Нью-Йорк. За його твердженням, граф не можна було забарвлювати менш ніж 5 кольорами, тим самим спростовуючи ще не підтверджену гіпотезу про те, що 4 кольори було достатньо, аби намалювати будь-який плоский граф. Те, що багато читачів не оцінили, це був місяць публікації випуску. Детальніше про цю історію можна знайти тут.
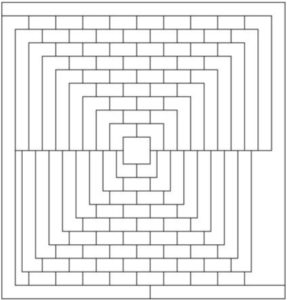
Ось граф, намальований як карта(малюнок)
Спроба декодувати можливе забарвлення цього графа як BDD насправді неможливо. Я вважаю, це займе більше одного мільярда вузлів (оскільки мінімальний графік має 20 вузлів в ширину, а для BDD потрібно швидко декодувати майже всі комбінації кольорів для цих вузлів).
Графічне фарбування як проблема SAT
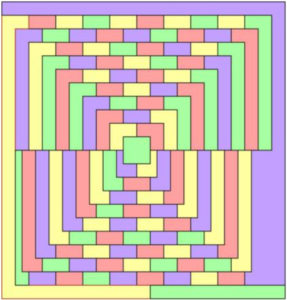
З іншого боку, розфарбування графу за допомогою рівняння для логічного виконання (SAT) цілком доцільно. Практикуючий повинен знайти лише одне можливе рішення, і тому він не стикається з серйозним завданням кодування всіх можливих кольорів. Ось колір, згенерований ZChaff solver, що працює протягом однієї секунди на портативному комп’ютері
Перегляньте відео з YouTube, яке демонструє, як відбувається пошук.
Також можна змусити розв’язувача генерувати «збалансоване» забарвлення, вимагаючи, щоб він знайшов рішення, використовуючи 2 кольори (зелений та синій) 27 разів і 2 кольори (червоний та жовтий) 28 разів.
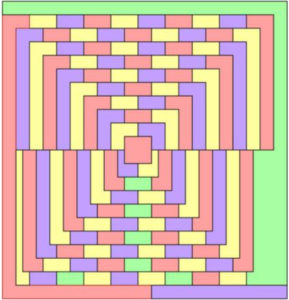
SAT solvers також можуть бути використані для вирішення проблем оптимізації шляхом виконання ряду викликів до розв’язувачів для виконання двозначного пошуку за цільовою функцією. Якщо ми попросимо вирішувача знайти колір, який спочатку мінімізує кількість вузлів зеленим кольором, потім мінімізуючи кількість синього кольору, а потім червоного, і ми отримуємо розмальовку лише з 7 зеленими, 34 синьо-червоними і 35 жовтими вузлами.
На основі подальших експериментів ми можемо стверджувати, що згідно з призначенням кольорів, це рішення має унікальні властивості:
- Це єдине забарвлення, де один колір використовується не більше 7 разів.
- Це єдине забарвлення, де один колір використовується принаймні 35 разів.


Добавить комментарий