Розмежування граничного шару є одним з найважливіших факторів, який визначає, наскільки добре функціонують літаки, кораблі, автомобілі, двигуни, мости, сучасні вітряні млини тощо. Вчені історично використовували круговий циліндр як спрощений «автомобіль», щоб спробувати зрозуміти, що відбувається. Наприклад, приблизно на початку цього століття німецькі вчені Ludwig Prandtl та H. Blasius вивчали граничний шар, який розвивається, коли циліндр починає рухатися. За допомогою експериментів та інноваційної математики вони довели, що граничний шар формується відразу біля поверхні рухомого циліндра. Це шар утворюється внаслідок тертя з поверхнею циліндра:
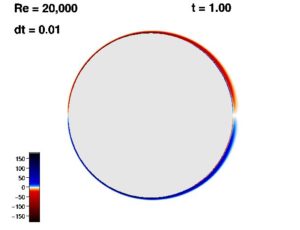
Прандтль і Блазіус вважали, що з часом цей граничний шар буде відокремлюватися від поверхні; у типових практичних застосувань це матиме катастрофічні наслідки для аеродинамічного опору, здатності до підйому, стабільності тощо.
В той же час, не було чітко зрозуміло, що спричинить перше відокремлення граничного шару від поверхні. Прандтль і Блазіус припускали, що це відбудеться, коли граничний шар розвине внутрішній шар поруч із поверхнею; в цьому шарі повітря або вода будуть обертатися в протилежному напрямку від решти граничного шару. Розподіл буде відбуватися на початку внутрішнього шару.
На сьогоднішній день, ми можемо виконати обчислення потоку і зробити ротацію видимою, використовуючи різні кольори. Це вже зроблено на попередньому знімку; подивись ще раз. На зображенні циліндр перемістився на відстань, що дорівнює половині його діаметра.
Зображення показує, що Прандтль і Блазіус мали рацію у внутрішніх шарах різної форми кольору; їх можна помітити з правого (підвітряного) боку циліндра. Відповідно до Прандтля і Блазіуса, поділ має відбуватися в крайніх лівих точках цих шарів. Фактично, це мало відбуватися набагато раніше, як тільки циліндр перемістився на одну шосту відстані свого діаметру. Складність полягає в тому, що здається, ніби ніяких змін по відношенню до поділу граничного шару з поверхні взагалі не відбувається. (Ідея Прандтля і Блазіуса виявилася корисною значно пізніше, коли розмежування граничного шару встигло розвинутися в повній мірі).
Коли відбувається поділ?
Це було у другій половині п’ятдесятих років коли обчислювальні гідродинаміки, такі як Френк Мур, Ніколас Ротт та Білл Сірс, дійсно почали помічати, що внутрішній підрівень не потребує відокремлення. Потрібно було щось краще, щоб вирішити, чи граничний шар дійсно відокремлюється від поверхні. Moore, а пізніше і значно сильніші Sears & Telionis, розвинули ідею про те, що «особливості рівнянь граничного шару» — це спосіб діагностувати самого розділення.
Тут необхідні пояснення. Рівняння граничного шару були відкриті Людвігом Прандтлом у 1904 р. як наближені до тих, що необхідні для обчислення потоку в тонких граничних шарах. Завдяки роботі Sidney Goldstein з Англії в 1948 році стало вірогідно, що рішення цих рівнянь припиняє своє існування, коли граничний шар відокремлюється. Точка, в якій рішення припиняє своє існування, називається сингулярністю.
Коротше кажучи, якщо ідеї Сірса і Теліоніса були правильними, то в рівняннях граничного шару для кругового циліндра мала бути сингулярність. Це, звичайно, було цікавим припущенням, але існувала одна суттєва проблема: численні рішення вже були доступні, і вони не показали жодної сингулярності! Здавалося, що знаходження рішення буде тривати вічно!
Чисельна перевірка теорії
Спочатку існували твердження, що сингулярність не враховувалася при попередніх розрахунках взагалі, але ці припущення так ніколи і не були доведені науковцями. Використовуючи найкращі численні методи, які лише він міг знайти, Tuncer Cebeci з корпорації McDonnell-Douglass вирахував найдовше рішення, але пройшло зовсім небагато часу із зображення вище і ніякої сингулярності він не виявив. Своє розчарування він зазначив у науковому журналі наступним чином:
Ми стверджуємо, що […] немає жодних підстав для твердження Сірса та Теліоніса про те, що [рівняння граничного шару] можуть розвинути сингулярність при кінцевому часі і навпаки, що подібні рішення взагалі існують для конкретного часу.
Tuncer Cebeci був правий у тому, що у часовому діапазоні, який він розраховував, не було сингулярності, хоча попередні автори і сказали, що є. Але це не означало, що її не буде і в майбутньому.
Тим часом, мій радник по докторантурі Шань-фу Шен і я дотримувався принципово іншого підходу. Ми розділили повітря навколо циліндра на дрібні шматочки і в цифрах відстежили рух кожної деталі. Це називається лагранжем підходом на честь італійського математика 18-го століття Йозефа Луї Лагранжа. Це дало змогу продовжувати обчислення протягом значно довшого проміжку часу, ніж будь-хто це робив раніше, і в результаті, ми знайшли сингулярність. Це відбулося після того, як циліндр перемістився на відстань три чверті свого діаметра. Порівняйте попередню картину, на якій циліндр перемістився на відстань половини свого діаметра, а на наступній — на повний діаметр:
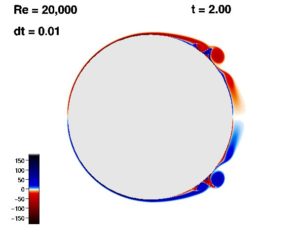
Ми представили наші результати на конференції в Польщі в 1977 році, і ми подали їх до відомого журналу Fluid Mechanics, але вони були категорично відхилені. Не найкраща мотивація для молодого аспіранта! Мені вдалося переконати професора Шена, що я абсолютно впевнений в тому, що все роблю правильно, і він ще раз надсилає категоричну відповідь до редакції, проте знову безрезультатно. Сам редактор відповів:
Вони не рекомендують відхилення через «неправильні обрахунки», вони це роблять, тому що вони не вважають це достатньо суттєвим внесок у розуміння; і лише один з них вказує на припущення, що деякі розбіжності можуть бути пов’язані з розрахунками.
(Перероблена версія була подана до журналу Journal of Computational Physics і з’явилася там в 1980 році. Тринадцять років потому журнал Fluid Mechanics опублікував наш із Стівеном Ковлі двосторонній документ про рішення та його застосування в більш загальних ситуаціях).
Незалежна підтримка
Першу підтримка наші розрахунки отримали в 1979 році від K. C. Wang, а потім у корпорації Мартіна Марієтта. Самостійно він отримав результати за допомогою звичайного чисельного методу, який запропонував розбити рішення приблизно в той же самий час, що і ми. На жаль, його розрахунки виявилися недостатньо точними, щоб переконати скептичних обчислювальих гідродинаміків.
Іще один аспірант на допомогу! Stephen Cowley з Англії намагався математично вирішити цю проблему. Незважаючи на те, що математичного рішення для рівнянь граничного шару немає, якщо будуть зроблені певні наближення у цьому напрямку, то і математичні рішення стануть можливими. І математики розробляють дуже розумні способи поліпшити такі наближення для того, щоб майже не існувало ніяких помилок. Використовуючи такі наближені підходи, Стівен виявив, що діапазон рішень, здавалось, закінчується саме в тому проміжку, де колись Шаньфу Шен і я знайшли свою сингулярність. Ми обмінялися записами, Стівен проклинав усе що можна (він хотів стати першим, хто зробив це відкриття!), але в тому, що чисельне і математичне рішення були абсолютно ідентичними, більше не виникало ніяких сумнівів.
З того моменту, інші автори повторно перераховували потік і підтверджували ці результати за допомогою інших, більш традиційних методів обчислення. Я все ще вірю, що якщо ви не знаєте, коли і де відбувається сингулярність, то єдиним і справді надійним методом є розрахунок Лагранжа. Проте обчислення Лагранжа набагато складніше, ніж звичайні обчислювальні процедури, і воно ще не стало популярним. Невелика група першопрохідців працює над тим, щоб змінити це, і в один прекрасний день всі наші обчислювальні точки можуть рухатися так само, як повітря.

Добавить комментарий