Дон Кнут працуе над 4-ым Томам Мастацтва камп’ютэрнага праграмавання. Адна з глаў, аб двайковых вырашальных дыяграмах і іх ужываннях, прадмет, які я знаходжу вельмі цікавым. Кнут паказвае, што разнастайнасць цікавых задач з тэорыі графаў можна закадаваць, як булевы формулы, а адукаваныя ДВД прадстаўляюць усе магчымыя рашэнні задачы. Часцей ёсць нейкі крытэрый аптымізацыі, і тады значна лягчэй выбраць «самае лепшае» рашэнне з ДВД простым дынамічным праграмуючым алгарытмам.
Тут мы паказваем прыклад выкарыстання графаў, якія прадстаўляюць 48 мяжуючых штатаў з кропкай перасячэння на кожным штаце і грань паміж двума штатамі, калі яны падзяляюць мяжу. На кожнай карце, калі вы націснеце на малюнак, адкрыецца дакумент у фармаце SVG. Вось граф, на якім размешчаны кропкі на сталіцах штатаў:

Туры па сталіцах
Выкажам здагадку, што вы хочаце наведаць 48 сталіц штатаў з умовай, што Вы праедзеце адзін штат толькі адзін раз. (Іншымі словамі, вы хочаце знайсці гамільтанаў шлях на графе.) Як відаць на карце вышэй, калі вы пойдзеце па самым прамым шляху паміж сталіцамі, то вы часцей будзеце перасякаць іншыя штаты, або, у выпадку напрамкі з Лензінга, Мічыган у Мэдысан, Вісконсін, вы праедзеце праз возера Мічыган. Замест гэтага Вы павінны выбраць самы кароткі шлях, які будзе звязваць два штата адной гранню. Давайце назавем такі шлях турам па сталіцах. Вось дыяграма мажлівага маршруту паміж штатамі:

Грунтуючыся на простым аналізе плюс спробах Кнута, мы можам сказаць наступнае:
- Усе туры павінны пачынацца або заканчвацца ў Мэне, паколькі ў Мэна адзіны сусед. Мы скарыстаемся Мэнам, як пачатковай кропкай.
- Усе туры павінны заканчвацца за межамі Нью-Ёрка, паколькі гэта кропка сучлянення.
- Усяго 68,656,026 розных тураў па сталіцах.
Вось самы кароткі тур па сталіцах, усяго 11,698 міль:

Вось самы доўгі тур па сталіцах, усяго 18, 040 міль:

Каляровы граф
Іншы цікавы клас задач ўключае ў сябе колеру карты. Правіла ў тым, каб ніякія мяжуючыя штаты не мелі адзін колер. Вядомая тэарэма аб чатырох колерах сцвярджае, што любы планарны граф можа мець да чатырох колераў.
Паколькі ДВД шыфруе ўсі магчымыя рашэнні ў булевы формулы, мы можам лёгка вылічыць, колькі ёсць рашэнняў. Для зафарбоўвання графа мы прыводзім у парадак нашы падлікі, каб выключыць сіметрыі з-за адвольнага прызначэння велічыні каляровай характарыстыкі (4! сіметрычных выпадку для 4 колераў).
Каб зафарбаваць мяжуючыя 48 штатаў, існуе 533,816,322,048 магчымых спосабаў. (Гэта ½ колькасці, прадстаўленага Кнутам, паколькі яго карта ўключае ў сябе Вашынгтон ДіСі, як 49-ы «штат», і ён можа быць запоўнены любым з двух колераў, не выкарыстаных для Мэрылэнда і Вірджыніі). Вось некалькі цікавых прыкладаў асаблівага зафарбоўвання:
- Збалансаванае зафарбоўванне, дзе кожны колер выкарыстоўваецца ў дакладнасці для 12 штатаў. Існуе 12,554,677,864 такіх зафарбоўванняў, што, на здзіўленне вышэй 2,4% усіх магчымых зафарбоўванняў.
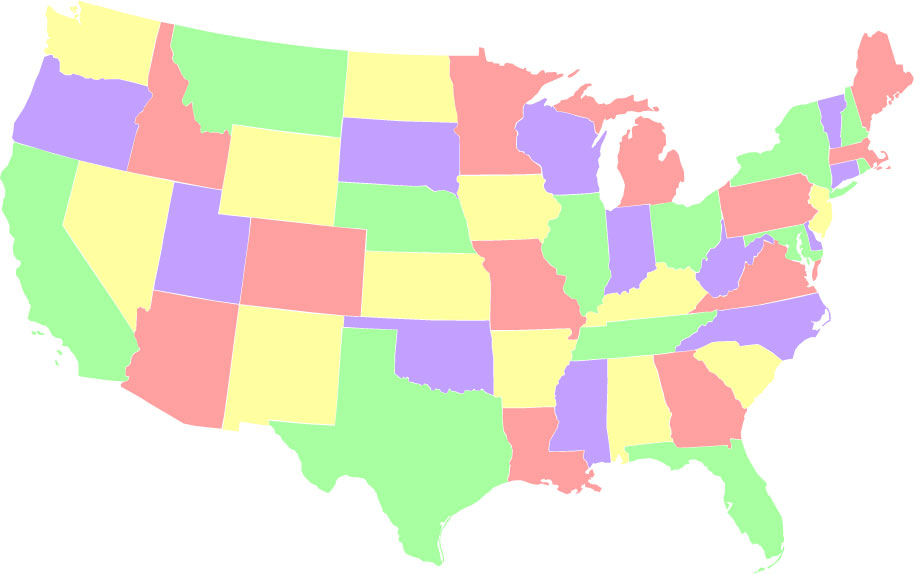
- *Незбалансаванае зафарбоўванне, дзе адзін з колераў (зялёны) выкарыстоўваецца так мала, як гэта магчыма (2 штата). Ёсць усяго толькі 288 спосабаў зафарбаваць карту так, каб адзін колер выкарыстоўваўся двойчы.

- *Незбалансаванае зафарбоўванне, у якім адзін колер (жоўты) выкарыстоўваецца так часта, як гэта магчыма (18 штатаў). Ёсць 71,002,368 спосабаў зафарбаваць карту так, каб адзін колер выкарыстоўваўся 18 разоў.
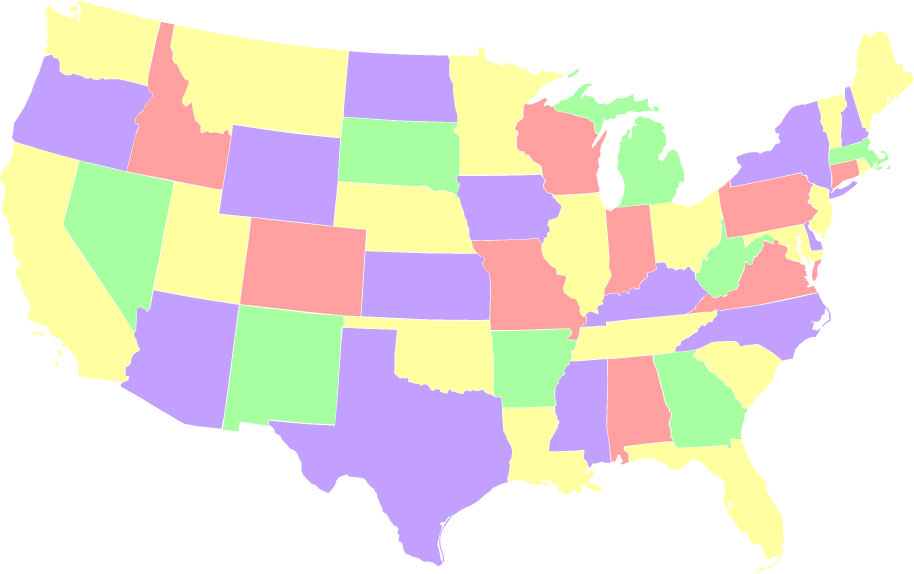
- Камбінаванне абодвух. Зафарбоўванне, выкарыстоўваючы колер 2, 13, 15 і 18 разоў. Гэтая паслядоўнасць: 1) злева направа, выкарыстоўваючы кожны колер у паслядоўнасці самую малую колькасць раз і 2) справа налева, выкарыстоўваючы кожны колер у паслядоўнасці самую вялікую колькасць разоў. Ёсць 24 такіх рашэнні.

З перспектывы праграм зафарбоўвання графа, карта 48-мі штатаў ЗША адносна простая. Паглядзіце вэб-старонку Граф МакГрегора, каб убачыць больш складаныя карты.

Добавить комментарий